Quantum entanglement is one of the central principles of, though it is also highly misunderstood. In short, quantum entanglement means that multiple particles are linked together in a way such that the measurement of one particle's quantum state determines the possible quantum states of the other particles. This connection isn't depending on the location of the particles in space. Epicmafia tree. Even if you separate entangled particles by billions of miles, changing one particle will induce a change in the other. Even though quantum entanglement appears to transmit information instantaneously, it doesn't actually violate the classical speed of light because there's no 'movement' through space.

One important thing to remember is that in quantum physics, the original uncertainty about the particle's quantum state isn't just a lack of knowledge. A fundamental property of quantum theory is that prior to the act of measurement, the particle really doesn't have a definite state, but is in a superposition of all possible states. This is best modeled by the classic quantum physics thought experiment, where a quantum mechanics approach results in an unobserved cat that is both alive and dead simultaneously.

Quantum entanglement is the physical phenomenon that occurs when a pair or group of particles is generated, interact, or share spatial proximity in a way such that the quantum state of each particle of the pair or group cannot be described independently of the state of the others, even when the particles are separated by a large distance.

P sym, but can always be described using local hidden variables. Moreover, it was shown that, for arbitrary numbers of parties, there exist states that are genuinely entangled but admit a local model. The mentioned proofs about the existence of local models assume that there is only one copy of the quantum state available at a time. If the parties are allowed to perform local measurements on many copies of such states, then many apparently local states (e.g., the qubit Werner states) can no longer be described by a local model. This is, in particular, true for all states.

However, it remains an open question whether all entangled states become non-local given sufficiently many copies.In short, entanglement of a state shared by two parties is necessary but not sufficient for that state to be non-local. It is important to recognize that entanglement is more commonly viewed as an algebraic concept, noted for being a prerequisite to non-locality as well as to and to, whereas non-locality is defined according to experimental statistics and is much more involved with the. Quantum mechanical frameworkThe following subsections are for those with a good working knowledge of the formal, mathematical description of, including familiarity with the formalism and theoretical framework developed in the articles:.

Pure statesConsider two noninteracting systems and, with respective s. The Hilbert space of the composite system is the. Scriptstyle 1 rangle A 0 rangle B.If the former occurs, then any subsequent measurement performed by Bob, in the same basis, will always return 1. If the latter occurs, (Alice measures 1) then Bob's measurement will return 0 with certainty. Thus, system has been altered by Alice performing a local measurement on system. This remains true even if the systems and are spatially separated.

This is the foundation of the.The outcome of Alice's measurement is random. Alice cannot decide which state to collapse the composite system into, and therefore cannot transmit information to Bob by acting on her system. Causality is thus preserved, in this particular scheme. For the general argument, see. EnsemblesAs mentioned above, a state of a quantum system is given by a unit vector in a Hilbert space. More generally, if one has less information about the system, then one calls it an 'ensemble' and describes it by a, which is a positive-semidefinite matrix, or a when the state space is infinite-dimensional, and has trace 1.

Again, by the, such a matrix takes the general form. alpha irangle. When a mixed state has rank 1, it therefore describes a 'pure ensemble'.

When there is less than total information about the state of a quantum system we need density matrices to represent the state.Experimentally, a mixed ensemble might be realized as follows. Consider a 'black box' apparatus that spits s towards an observer. The electrons' Hilbert spaces are. The apparatus might produce electrons that are all in the same state; in this case, the electrons received by the observer are then a pure ensemble. However, the apparatus could produce electrons in different states.

For example, it could produce two populations of electrons: one with state. Brhoiare themselves pure ensembles. A state is then said to be entangled if it is not separable.In general, finding out whether or not a mixed state is entangled is considered difficult. The general bipartite case has been shown to be. For the and cases, a necessary and sufficient criterion for separability is given by the famous condition.

Reduced density matricesThe idea of a reduced density matrix was introduced by in 1930. Consider as above systems and each with a Hilbert space. Let the state of the composite system be. Rho A = psirangle A langlepsi A.In general, a bipartite pure state ρ is entangled if and only if its reduced states are mixed rather than pure. Two applications that use themReduced density matrices were explicitly calculated in different spin chains with unique ground state.

An example is the one-dimensional: the ground state can be divided into a block and an environment. The reduced density matrix of the block is to a projector to a degenerate ground state of another Hamiltonian.The reduced density matrix also was evaluated for, where it has full rank. It was proved that in the thermodynamic limit, the spectrum of the reduced density matrix of a large block of spins is an exact geometric sequence in this case.

Entanglement as a resourceIn quantum information theory, entangled states are considered a 'resource', i.e., something costly to produce and that allows to implement valuable transformations. The setting in which this perspective is most evident is that of 'distant labs', i.e., two quantum systems labeled 'A' and 'B' on each of which arbitrary s can be performed, but which do not interact with each other quantum mechanically. The only interaction allowed is the exchange of classical information, which combined with the most general local quantum operations gives rise to the class of operations called (local operations and classical communication). These operations do not allow the production of entangled states between the systems A and B. But if A and B are provided with a supply of entangled states, then these, together with LOCC operations can enable a larger class of transformations. For example, an interaction between a qubit of A and a qubit of B can be realized by first teleporting A's qubit to B, then letting it interact with B's qubit (which is now a LOCC operation, since both qubits are in B's lab) and then teleporting the qubit back to A. Two maximally entangled states of two qubits are used up in this process.

Thus entangled states are a resource that enables the realization of quantum interactions (or of quantum channels) in a setting where only LOCC are available, but they are consumed in the process. There are other applications where entanglement can be seen as a resource, e.g., private communication or distinguishing quantum states.

Classification of entanglementNot all quantum states are equally valuable as a resource. To quantify this value, different entanglement measures (see below) can be used, that assign a numerical value to each quantum state. However, it is often interesting to settle for a coarser way to compare quantum states. This gives rise to different classification schemes. Most entanglement classes are defined based on whether states can be converted to other states using LOCC or a subclass of these operations. The smaller the set of allowed operations, the finer the classification. Important examples are:.

If two states can be transformed into each other by a local unitary operation, they are said to be in the same LU class. This is the finest of the usually considered classes. Two states in the same LU class have the same value for entanglement measures and the same value as a resource in the distant-labs setting. There is an infinite number of different LU classes (even in the simplest case of two qubits in a pure state). If two states can be transformed into each other by local operations including measurements with probability larger than 0, they are said to be in the same 'SLOCC class' ('stochastic LOCC'). Qualitatively, two states.

Rhointo at least one pure entangled state. States that have this property are called. These states are the most useful quantum states since, given enough of them, they can be transformed (with local operations) into any entangled state and hence allow for all possible uses. Rho log 2 rho = int λ log 2 λ d P λ.As in, the more uncertainty (number of microstates) the system should possess, the larger the entropy. For example, the entropy of any pure state is zero, which is unsurprising since there is no uncertainty about a system in a pure state.

The entropy of any of the two subsystems of the entangled state discussed above is (which can be shown to be the maximum entropy for mixed states). As a measure of entanglementEntropy provides one tool that can be used to quantify entanglement, although other entanglement measures exist. If the overall system is pure, the entropy of one subsystem can be used to measure its degree of entanglement with the other subsystems.For bipartite pure states, the von Neumann entropy of reduced states is the unique measure of entanglement in the sense that it is the only function on the family of states that satisfies certain axioms required of an entanglement measure.It is a classical result that the Shannon entropy achieves its maximum at, and only at, the uniform probability distribution. Therefore, a bipartite pure state is said to be a maximally entangled state if the reduced state of is the diagonal matrix.

Take a crack at the most downloaded trivia game! Prove you are the smartest one not only by answering trivial questions, but by suggesting multiple-choice questions. Test your knowledge in six different categories led by exciting characters. For all fans logic games such as Trivia Crack, QuizUp and logo quiz!Step up your quiz game answering fun general knowledge trivia questions!Challenge your friends and family to fun trivia questions! Spin Willy the Wheel and let fate decide where to start your quiz question game.Show the world how clever you are while you learn new and interesting facts with the world’s best trivia app.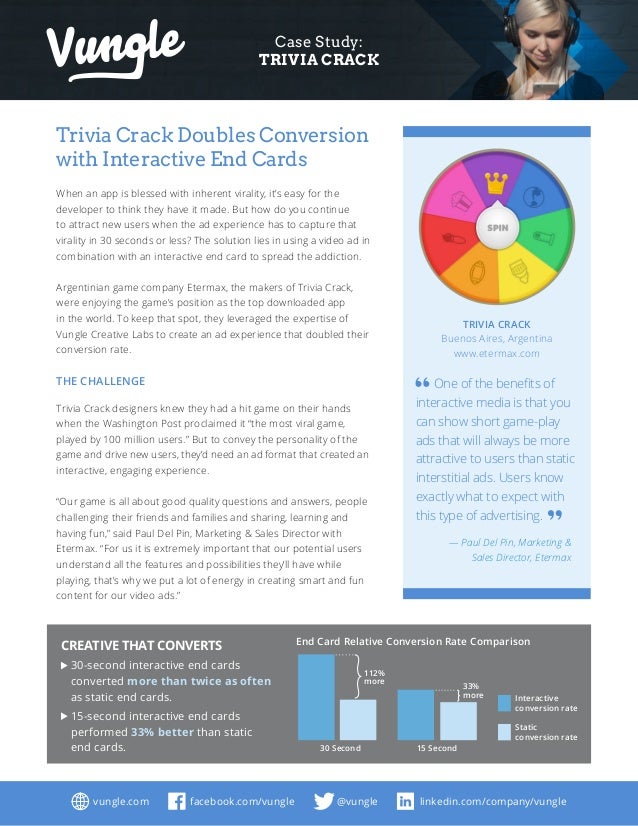

U(t) = exp left(- i H thbarright),where is the of the system. Here the entropy is unchanged.The reversibility of a process is associated with the resulting entropy change, i.e., a process is reversible if, and only if, it leaves the entropy of the system invariant.

Therefore, the march of the towards is simply the growing spread of quantum entanglement. This provides a connection between quantum information theory and.also can be used as a measure of entanglement. Entanglement measuresEntanglement measures quantify the amount of entanglement in a (often viewed as a bipartite) quantum state. As aforementioned, is the standard measure of entanglement for pure states (but no longer a measure of entanglement for mixed states). For mixed states, there are some entanglement measures in the literature and no single one is standard.

Entanglement cost. Entanglement of formation. Logarithmic negativityMost (but not all) of these entanglement measures reduce for pure states to entanglement entropy, and are difficult to compute. Quantum field theoryThe of is sometimes seen as an analogue of quantum entanglement.

ApplicationsEntanglement has many applications in quantum information theory. With the aid of entanglement, otherwise impossible tasks may be achieved.Among the best-known applications of entanglement are and.Most researchers believe that entanglement is necessary to realize (although this is disputed by some).Entanglement is used in some protocols of. This is because the 'shared noise' of entanglement makes for an excellent. Moreover, since measurement of either member of an entangled pair destroys the entanglement they share, entanglement-based quantum cryptography allows the sender and receiver to more easily detect the presence of an interceptor.In, entanglement is necessary for surpassing the and achieving the.

Entangled statesThere are several canonical entangled states that appear often in theory and experiments.For two, the s are. Psi + rangleexcept the basis kets 0 and 1 have been replaced with 'the N photons are in one mode' and 'the N photons are in the other mode'.Finally, there also exist twin Fock states for bosonic modes, which can be created by feeding a into two arms leading to a beam splitter. They are the sum of multiple of NOON states, and can used to achieve the Heisenberg limit.For the appropriately chosen measure of entanglement, Bell, GHZ, and NOON states are maximally entangled while spin squeezed and twin Fock states are only partially entangled. The partially entangled states are generally easier to prepare experimentally.

Methods of creating entanglementEntanglement is usually created by direct interactions between subatomic particles. These interactions can take numerous forms. One of the most commonly used methods is to generate a pair of photons entangled in polarisation. Other methods include the use of a to confine and mix photons, photons emitted from decay cascade of the bi-exciton in a, the use of the, etc., In the earliest tests of Bell's theorem, the entangled particles were generated using s.It is also possible to create entanglement between quantum systems that never directly interacted, through the use of entanglement swapping. Two independently-prepared, identical particles may also be entangled if their wave functions merely spatially overlap, at least partially. Testing a system for entanglementA density matrix ρ is called if it can be written as a convex sum of product states, namely.

1 ge p jge 0probabilities. By definition, a state is entangled if it is not separable.For 2-Qubit and Qubit-Qutrit systems (2 × 2 and 2 × 3 respectively) the simple provides both a necessary and a sufficient criterion for separability, and thus -inadvertently- for detecting entanglement.

However, for the general case, the criterion is merely a necessary one for separability, as the problem becomes when generalized. Other separability criteria include (but not limited to) the, and those based on uncertainty relations. For a review of separability criteria in discrete variable systems.A numerical approach to the problem is suggested by, and Eirik Ovrum in their paper 'Geometrical aspects of entanglement'. Leinaas et al. Offer a numerical approach, iteratively refining an estimated separable state towards the target state to be tested, and checking if the target state can indeed be reached. An implementation of the algorithm (including a built-in testing) is web-app.In continuous variable systems, the also applies. Specifically, Simon formulated a particular version of the Peres-Horodecki criterion in terms of the second-order moments of canonical operators and showed that it is necessary and sufficient for.